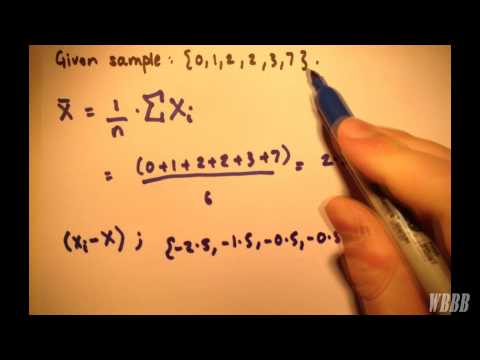
Inhoud
Een cruciale stap in veel statistische analyses is de berekening van de som van kwadraten van afwijkingen van het gemiddelde, soms aangeduid als de berekening van de som van vierkanten. U kunt het resultaat van deze berekening krijgen met elke formule die een som van vierkanten gebruikt.
routebeschrijving

-
Bereken het gemiddelde van uw lijst met nummers. Tel alle waarden bij elkaar op en deel het resultaat door het totale aantal in uw lijst.
-
Trek het gemiddelde dat u zojuist hebt gevonden af van elk nummer in de oorspronkelijke lijst. Dit levert verschillende negatieve cijfers op, maar geen probleem. Deze lijst wordt de "Afwijkingen van het gemiddelde" genoemd.
-
Zet alle nummers in je nieuw aangepaste lijst met afwijkingen van het gemiddelde vierkant. Onthoud dat om een getal in het kwadraat te verhogen, het eenvoudigweg alleen vermenigvuldigt. Omdat dit alleen een positief cijfer oplevert, moeten alle nummers in uw nieuwe lijst positief zijn. Het is de lijst met vierkanten van afwijkingen van het gemiddelde.
-
Voeg alle getallen in de lijst met kwadraten van afwijkingen van het gemiddelde toe. Het resultaat wordt de som van kwadraten van afwijkingen genoemd en kan in elke formule worden gebruikt waarvoor een som van vierkanten als een van de termen is vereist.